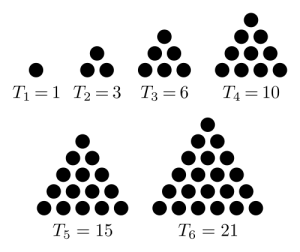
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, …
Triangular numbers
Triangular numbers are a beautiful thing. It is a visual pattern, a numeric pattern, and there is a nice algebraic function. The is the mathematical trifecta we love.
Videos
My introduction to triangular numbers (at the 1:12 minute mark, to 4:58)
Video by a school student on triangular numbers
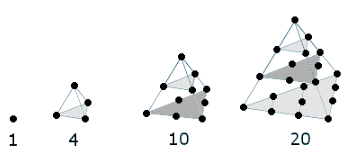
Introduction to tetrahedral numbers, which are made up of triangles (at the 6:49 mark).
Useful
The triangular numbers are useful.
They answer the Handshake Question: If 12 people are in a room and each person shakes hands with every other person once, how many handshakes are there? A: 
This can be used anytime you have to find out how many pairings there are. For example for a recreation volleyball or softball league.
The formula (function) to find the nth triangular number is 
Webpages
Triangular Number Sequence – from MathIsFun.
Fascinating Triangular Numbers
Tetrahedral numbers
Recent Comments