Various pages on three-dimensional solids.
3D Solids
Platonic and Archimedean Solids
This is a intended to be a steady stream of cool ideas about Platonic and Archimedean Solids. **Page under construction** It Starts with the Tetrahedron The tetrahedron is awesome. It has 4 triangles for faces, 4 vertices, and 6 edges. A vertex is a point (0-dimensional). An edge is a segment (1-D). A face is …
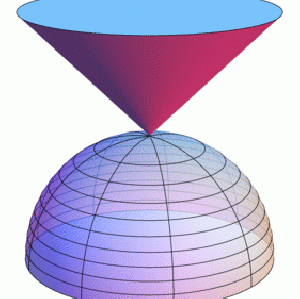
Cone, Hemisphere, Cylinder Relationship
Volumes The ratio of the volumes of Cone:Hemisphere:Cylinder is 1:2:3. Make each with a radius of r and and height of r. (The formulas work out nicely. This is left to the reader as a nice exercise 😉 Here’s a nice gif of the concept (click to see the animation): This was found on a …
Top 9 Interesting Things to Know about the Rhombic Triacontahedron
Rhombic Triacontahedron The Rhombic Triacontahedron is made up of 30 rhombi (rhombuses). Every face is congruent. The Rhombic Triacontahedron is not Platonic (that’s obvious, there are only 5 Platonic solids), not Archimedean, and not even a Johnson solid, because the faces are not regular polygons. The shape is so interesting that it is sold as …
Burr Puzzle – Origami !!
The 6-piece Octagonal Ball Burr Puzzle is a classic puzzle, usually made of wood. It has 6 congruent pieces. They fit together (quite easily, really) into a ‘ball.’ Two in the x-direction; Two in the y-direction; and (or course) Two in the z-direction. This can be made of paper. Origami. During the COVID-19 stay-at-home order, …
Origami Icosahedron
Annie Perkins (@anniek_p) shared (Twitter) how to make an icosahedron out of paper. (BTW, her video really helps.) I had to make one. It turns out that the edges can be colored, using 5 colors, so that the 5 edges meeting at every vertex are all different. I used 5 colors. Picked Easter colors! 6 …
Origami: Unit Options
This page should probably be titled Unit Origami Options. This page is under construction. I want a place to put links to the various ways to do Unit Origami. Unit Origami from Unfolding Mathematics with Unit Origami Similar (but different) to the Sonobe unit. Very versatile. Sonobe Unit Origami this is very common and very …
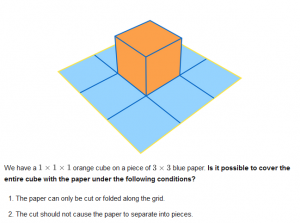
9-Grid Cube Problem
Here is an interesting problem from Week May 15 (2017) from https://brilliant.org/ https://brilliant.org/weekly-problems/2017-05-15/basic/?p=5 [Answer: It is possible.] My daughter and I worked on this problem and discovered a few interesting things. [As background: If you are unfamiliar with nets for a cube, you might want to visit http://mathforum.org/library/drmath/view/54682.html ] Our solution is below. Save …
Undergraduate Research Project Ideas
Here are a few ideas for undergraduate research projects involving three-dimensional geometry. Understanding dihedral angles. How to measure them from all the ways the angle may be presented. How points lines and planes are represented in 3 dimensions. Szilassi polyhedron – http://www.thingiverse.com/thing:12200 http://themathkid.tumblr.com/post/153564454406/57crazylittlethings-twocubes-apparently other coloring results in 3-dimensions.
Why is Volume of a Pyramid one-third the Prism?
This vides shows why the volume of a pyramid is 1/3 of the volume of the prism with the same base and same height. This can be done using the solids in the Math Resource Office (MRO) at Western Illinois University.
Permutohedron
See this Google Doc: https://docs.google.com/document/d/1Er2FKMK9ZVuY4a0k60qZw2LRlBdtGES9DfgyXBD43pk/edit?usp=sharing A permutohedron is a real thing — even on Wikipedia.
Recent Comments