May 11
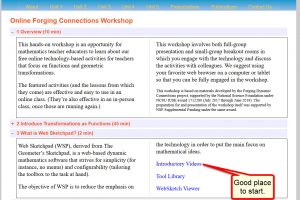
I attended (5/11/2020) a 2 hour webinar that was very good. It was very good. They have good goals and good guiding principles. https://geometricfunctions.org/fc/ is the main website. Workshop agenda and links are here: https://geometricfunctions.org/fc/present/online-workshop-05-11-2020/ For Web Sketchpad (this is a free, web, version of Geometer’s Sketchpad, see the graphic for a good place to …
Jul 11
Jun 07
KaleidoTile is a colorful program for investigating Tilings, Symmetry, and Polyhedra. I remember seeing it many years ago. I’m glad to see that Jeff Weeks is continuing to update it. FREE download. http://geometrygames.org/KaleidoTile/index.html
Oct 30
Update: I turned this into a full page: Top 8 Interesting Things to Know about the Rhombic Triacontahedron Ball of Whacks is a geometry toy. (Available online and in toy stores that sell cool stuff.) It is a rhombic triacontahedron. Each of the 30 rhombic faces are golden, in that the ratio of the diagonals …
Oct 25
Jun 08
Beauty of Three Dimensional Polyhedra Workshop (in Celebration of the MAA’s Centennial) MathFest at Washington, DC. Friday, August 7, 2015, 1:00-2:20 p.m., Maryland C Description: I have long been fascinated by the Platonic and Archimedean solids and their mathematical beauty. In this workshop I will demonstrate, and we will work with, a variety of materials …
Recent Comments