Counting Squares in a Staircase and Triangles Made of Matchsticks
A beautiful relationship
Background
This all started with a tweet from @KiranABacche: https://twitter.com/KiranABacche/status/1340575537845002276?s=20
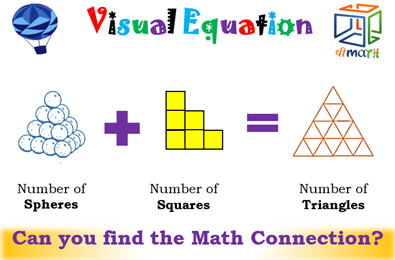 I worked on it for half an hour and couldn’t make sense of it. So I tweeted that it seemed to have problems. Clarification tweets came in. In particular, that one needs to count all the squares and all the triangles. So, a couple weeks later I dug into the problem.
I worked on it for half an hour and couldn’t make sense of it. So I tweeted that it seemed to have problems. Clarification tweets came in. In particular, that one needs to count all the squares and all the triangles. So, a couple weeks later I dug into the problem.
It is a Nice Result!
It turns out that it is a general principle.
Why it is true (video below) is very nice and helps us understand the square counting and the triangle counting problems better.
The formula (function) for the tetrahedral numbers is very clean and nice. The functions for the number of squares and number of triangles are not so clean, but there are numerous (and varied and interesting) ways to get formulas. This is instructive in understanding functions.
Desmos
I made a Desmos file that shows the result numerically, using various ways to define the three functions:
- T(n) = the nth tetrahedral number;
- S(n) = the number of squares (any size) in a staircase of n steps built with unit squares;
- M(n) = the number of triangles in a triangular matchstick arrangement of side n.
In the Desmos file I defined the functions in three ways: “polynomial-like,” using the floor function, and piecewise defined.
The result is that T(n) + S(n-1) = M(n) (as demonstrated in the Desmos file).
But Why?
I made a video which visually shows why the result is true.
It is useful to know a little bit about Triangular numbers.
GeoGebra
I made two GeoGebra files to investigate.
- Staircase Squares – Use this to think about S(n).
- Matchstick Triangles – Use this to think about M(n).
References
More information on the three sequences can be found at the The On-Line Encyclopedia of Integer Sequences (oeis.org)

Recent Comments